Asking fundamental questions

Source: Quanta, May 2023

In 1928, the German mathematicians David Hilbert and Wilhelm Ackermann proposed a question called the Entscheidungsproblem (“decision problem”). In time, their question would lead to a formal definition of computability, one that allowed mathematicians to answer a host of new problems and laid the foundation for theoretical computer science.

The definition came from a 23-year-old grad student named Alan Turing, who in 1936 wrote a seminal paper that not only formalized the concept of computation, but also proved a fundamental question in mathematics and created the intellectual foundation for the invention of the electronic computer.

Turing’s great insight was to provide a concrete answer to the computation question in the form of an abstract machine, later named the Turing machine by his doctoral adviser, Alonzo Church. It’s abstract because it doesn’t (and can’t) physically exist as a tangible device. Instead, it’s a conceptual model of computation: If the machine can calculate a function, then the function is computable.

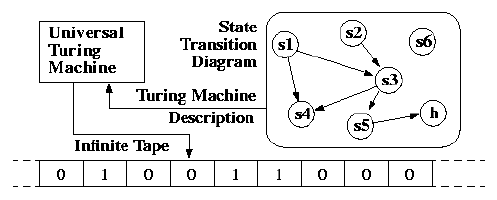
https://web.mit.edu/manoli/turing/www/turing.html

With his abstract machine, Turing established a model of computation to answer the Entscheidungsproblem, which formally asks: Given a set of mathematical axioms, is there a mechanical process — a set of instructions, which today we’d call an algorithm — that can always determine whether a given statement is true?

in 1936, Church and Turing — using different methods — independently proved that there is no general way of solving every instance of the Entscheidungsproblem. For example, some games, such as John Conway’s Game of Life, are undecidable: No algorithm can determine whether a certain pattern will appear from an initial pattern.

“I think it is commonly accepted that the Church-Turing thesis says that the informal notion of algorithm corresponds to what any ‘reasonable’ computational model can do.” Other mathematicians have come up with different models of computation that look quite different on the surface but are actually equivalent: They can do any computation that Turing machines can do, and vice versa.

Only a few years after Kurt Gödel had proved that mathematics was incomplete, Church and Turing showed with this work that some problems in mathematics are undecidable — no algorithm, however sophisticated, can tell us whether the answer is yes or no. Both were devastating blows to Hilbert, who had hoped mathematics would have tidy, idealized answers. But it’s perhaps just as well: If a general solution to the Entscheidungsproblem existed, it would mean that all problems in mathematics could be reduced to simple mechanical calculations.

Sanjeev Arora, a theoretical computer scientist at Princeton University …  emphasizes a broader philosophical picture.

“There’s two notions of ‘universal,’” he said. “One notion of the universal is that it can run any other Turing machine. But the other, bigger notion of ‘universal’ is that it can run any computation that you will come up with in the universe.” In the world of classical physics, any physical process can be modeled or simulated using algorithms, which, in turn, can be simulated by a Turing machine.”

asking fundamental questions can be among the most useful things a scientist can do.

ARM China – IP Theft

Source: SemiAnalysis/Substack, Aug 2021

Arm is widely regarded as the most important semiconductor IP firm. Their IP ships in billions of new chips every year from phones, cars, microcontrollers, Amazon servers, and even Intel’s latest IPU. Originally it was a British owned and headquartered company, but SoftBank acquired the firm in 2016. They proceeded to plow money into Arm Limited to develop deep pushes into the internet of things, automotive, and server. Part of their push was also to go hard into China and become the dominant CPU supplier in all segments of the market.

As part of the emphasis on the Chinese market, SoftBank succumbed to pressure and formed a joint venture. In the new joint venture, Arm Limited, the SoftBank subsidiary sold a 51% stake of the company to a consortium of Chinese investors for paltry $775M. This venture has the exclusive right to distribute Arm’s IP within China. Within 2 years, the venture went rogue. Technically it has always been legally independent, but Arm still maintained control. Recently, Arm China gave a presentation to the industry about rebranding their own IP, extending it by developing more, and emphasizing that they are striking their own independently operated path.

This firm is called “安谋科技”, but it is not part of Arm Limited.

This is the tech heist of the century.

Arm China, 安谋科技, is asserting their independence. It is the most publicized instance of a joint venture in China going rogue, but also the most dangerous one. The Arm China board is not in agreeance with Allen Wu, but he still holds power despite his formal removal. Minority stake joint ventures have had control wrestled away from the parent company, but this may be the most brazen attempt yet.

Arm has been shaken to its core with the 2nd largest market snatched from underneath it. According to Arm, no IP has been stolen, but Arm cannot license directly license to any firm in China. They must go through 安谋科技.

DELPHI: an MIT framework using machine learning to estimate the impact of a scientific article

Source: Nature, May 2021

The scientific ecosystem relies on citation-based metrics that provide only imperfect, inconsistent and easily manipulated measures of research quality.

Here we describe DELPHI (Dynamic Early-warning by Learning to Predict High Impact), a framework that provides an early-warning signal for ‘impactful’ research by autonomously learning high-dimensional relationships among features calculated across time from the scientific literature.

We prototype this framework and deduce its performance and scaling properties on time-structured publication graphs from 1980 to 2019 drawn from 42 biotechnology-related journals, including over 7.8 million individual nodes, 201 million relationships and 3.8 billion calculated metrics.

We demonstrate the framework’s performance by correctly identifying 19/20 seminal biotechnologies from 1980 to 2014 via a blinded retrospective study and provide 50 research papers from 2018 that DELPHI predicts will be in the top 5% of time-rescaled node centrality in the future.

We propose DELPHI as a tool to aid in the construction of diversified, impact-optimized funding portfolios.

Related Resource: Actuia, May 2021

James W. Weis, a research associate at the MIT Media Lab, and Joseph Jacobson, a professor in the Media Arts & Sciences program and head of the Media Lab’s Molecular Machines research group, have published an article about the tool they developed: the Dynamic Early-warning by Learning to Predict High Impact ( DELPHI) framework.

This is a machine learning algorithm that takes into account numerous scientific articles. The researchers wanted to exploit this database, which has been growing steadily since the 1980s. The model was developed using a complete chronological compilation of articles that does not only take into account the number of citations of the publication, but all the available metadata allowing to really grasp the propagation of this information in the scientific world.

James W. Weis explains how the tool works:

“Essentially, our algorithm works by learning patterns from scientific history, then matching those patterns on new publications to try to identify early high-impact signals.

By tracking the early diffusion of ideas from these new papers, we can predict how likely publications are to go viral or likely to spread to the broader academic and scientific community in a meaningful way.”

The result is a graph containing several connections: they correspond to citations to an article. At the end of both ends of the connection are the nodes that contain all the information of a publication: content, authors, institutions, etc. The more a node is in the center of the graph and causes the creation of new connections, the more the publication is considered to have a strong impact.

Thanks to this system, the scientific impact of the articles is estimated and the articles located in the center of the graph, up to 5% of the nodes, are considered as “high impact”. 5% is the base value, but it can be adjusted between 1 and 10% of the nodes.

A system that deduces the high potential impact of an article

From the generated graphs, DELPHI suggests that high-impact articles propagate on a large scale: to small scientific communities, and even in fields not necessarily related to the one of publication. DELPHI considers that between two papers with the same number of citations, the one with the highest impact is the one that reaches the widest audience. However, even if the programme succeeds in identifying and valorising articles considered as having an impact, publications with a lower impact are not really exploited.

James W. Weis, one of the project’s two investigators, discusses the possible uses of its creation:

“The framework could be useful to encourage teams to work together, even if they don’t know each other. For example, it could make it easier for them to manage their funds with each other to get together and work on important multidisciplinary problems.”

Joseph Jacobson, the second researcher, refers to the objectives of this study:

“This study was about whether it was possible to create a process in a more scalable way, using the scientific community as a whole, as embedded in the academic graph, and being more inclusive in identifying high-impact research directions.”

The researchers caution, however, that DELPHI does not predict the future. Machine learning is used to extract and quantify signals present in the data set. Nevertheless, they were surprised at how quickly an article can be considered high-impact.

A model used to discover the gem of scientific publications

DELPHI was used to highlight about 50 scientific publications that would have a high impact by 2023. Several fields are covered: nanorobots used for cancer treatment, deep neural networks to help chemistry, new discoveries around lithium batteries, etc.

The two researchers believe that DELPHI will be a tool that can help institutions, governments and other decision-makers better manage investments in scientific research. The model will identify technologies that are considered “rare gems” of modern science, which could guide decision-makers to make the right choices.

This is an aspect also mentioned by James W. Weis:

“I became increasingly aware that investors, including myself, were constantly looking for new companies in the same places and with the same preconceptions around research.

Yet there is a huge wealth of highly talented people and incredible technologies that I began to glimpse, but that many were overlooking.

I thought there had to be a way to work in this space and that machine learning could help us find all this untapped potential more efficiently.”

Bank of England Releases Alan Turing banknote

Source: Bank of England website, 2021

The design on the reverse of the note celebrates Alan Turing and his pioneering work with computers. It features:

• A mathematical table and formulae from Turing’s seminal 1936 paper “On Computable Numbers, with an application to the Entscheidungsproblem” Proceedings of the London Mathematical Society. This paper is widely recognised as being foundational for computer science.
• The Automatic Computing Engine (ACE) Pilot Machine which was developed at the National Physical Laboratory as the trial model of Turing’s pioneering ACE design. The ACE was one of the first electronic stored-program digital computers.
• Ticker tape depicting Alan Turing’s birth date (23 June 1912) in binary code.
• Technical drawings for the British Bombe, the machine specified by Turing and one of the primary tools used to break Enigma-enciphered messages during WWII.
• The flower-shaped red foil patch on the back of the note is based on the image of a sunflower head linked to Turing’s morphogenetic (study of patterns in nature) work in later life.
• A series of background images, depicting technical drawings from The ACE Progress Report.

Google Chrome’s Privacy Challenges

Source: Forbes, Mar 2021

Chrome collects your user ID and device ID in too many categories. Unlike Safari, Edge and Firefox, Chrome says it links all harvested data to devices and individuals. Safari collects but doesn’t link browsing history, usage data and locations to users. Neither Firefox nor Edge link usage data. But Chrome says it collects all those data fields and links all of them to user identities.

Chrome collects more data than any of the other browsers, yet is the only one that doesn’t appear to collect any data that isn’t linked to user identities. This is a much more shocking illustration of the different philosophies at play. Chrome hasn’t even attempted to protect its users’ privacy in this way. This isn’t about specific data fields, this is about an overarching attitude to privacy.

Avi Wigderson: Co-Winner of 2021 Abel Prize

Source: Abel Prize website, Mar 2021

Wigderson is known for his ability to see links between apparently unrelated areas. He has deepened the connections between mathematics and computer science. He was born in Haifa, Israel, in 1956. His contribution to enlarging and deepening the field of ‘complexity theory’ – which concerns itself with the speed and efficiency of algorithms – is arguably greater than that of any single other person.

Wigderson has conducted research into every major open problem in complexity theory. In many ways, the field has grown around him. He has co-authored papers with more than 100 people.

The most important present-day application of complexity theory is internet cryptography. Early in his career Wigderson made fundamental contributions in this area, including the zero-knowledge proof, which today is being used in cryptocurrency technology.

In 1994, Wigderson won the Rolf Nevanlinna Prize for com

https://www.ias.edu/scholars/wigderson

His main research area is computational complexity theory. This field studies the power and limits of efficient computation and is motivated by such fundamental scientific problems as:

Does P = NP?

(Can mathematical creativity be efficiently automated?

His 2019 “Mathematics and Computation”

Kurt Godel’s Letter to John von Neumann

Source: Genderi.org, date indeterminate

English translation (1st known NP-complete problem)

The Gödel Letter

Princeton, 20 March 1956

Dear Mr. von Neumann:

With the greatest sorrow I have learned of your illness. The news came to me as quite unexpected. Morgenstern already last summer told me of a bout of weakness you once had, but at that time he thought that this was not of any greater significance. As I hear, in the last months you have undergone a radical treatment and I am happy that this treatment was successful as desired, and that you are now doing better. I hope and wish for you that your condition will soon improve even more and that the newest medical discoveries, if possible, will lead to a complete recovery.

Since you now, as I hear, are feeling stronger, I would like to allow myself to write you about a mathematical problem, of which your opinion would very much interest me: One can obviously easily construct a Turing machine, which for every formula F in first order predicate logic and every natural number n, allows one to decide if there is a proof of F of length n (length = number of symbols). Let ψ(F,n) be the number of steps the machine requires for this and let φ(n) = maxF ψ(F,n). The question is how fast φ(n) grows for an optimal machine. One can show that φ(n) ≥ k ⋅ n. If there really were a machine with φ(n) ∼ k ⋅ n (or even ∼ k ⋅ n²), this would have consequences of the greatest importance. Namely, it would obviously mean that in spite of the undecidability of the Entscheidungsproblem, the mental work of a mathematician concerning Yes-or-No questions could be completely replaced by a machine. After all, one would simply have to choose the natural number n so large that when the machine does not deliver a result, it makes no sense to think more about the problem. Now it seems to me, however, to be completely within the realm of possibility that φ(n) grows that slowly. Since it seems that φ(n) ≥ k ⋅ n is the only estimation which one can obtain by a generalization of the proof of the undecidability of the Entscheidungsproblem and after all φ(n) ∼ k ⋅ n (or ∼ k ⋅ n²) only means that the number of steps as opposed to trial and error can be reduced from N to log N (or (log N)²). However, such strong reductions appear in other finite problems, for example in the computation of the quadratic residue symbol using repeated application of the law of reciprocity. It would be interesting to know, for instance, the situation concerning the determination of primality of a number and how strongly in general the number of steps in finite combinatorial problems can be reduced with respect to simple exhaustive search.

I do not know if you have heard that “Post’s problem”, whether there are degrees of unsolvability among problems of the form (∃ y) φ(y,x), where φ is recursive, has been solved in the positive sense by a very young man by the name of Richard Friedberg. The solution is very elegant. Unfortunately, Friedberg does not intend to study mathematics, but rather medicine (apparently under the influence of his father). By the way, what do you think of the attempts to build the foundations of analysis on ramified type theory, which have recently gained momentum? You are probably aware that Paul Lorenzen has pushed ahead with this approach to the theory of Lebesgue measure. However, I believe that in important parts of analysis non-eliminable impredicative proof methods do appear.

I would be very happy to hear something from you personally. Please let me know if there is something that I can do for you. With my best greetings and wishes, as well to your wife,

Sincerely yours,

Kurt Gödel

P.S. I heartily congratulate you on the award that the American government has given to you.

Related Resource: MIT “Great Ideas in Theoretical Computer Science”, Spring 2008

Is there a better way to solve the problem that doesn’t involve a brute-force search? Exactly this question was asked in one of the most remarkable documents in the history of theoretical computer science: a letter that Kurt G¨odel sent to John von Neumann in 1956. (The full text of this letter is in the appendix.)

In this letter, G¨odel concludes that if there were some general way to avoid brute-force search, mathematicians would be out of a job! You could just ask your computer whether there’s a proof of Goldbach, the Riemann Hypothesis, etc. with at most a billion symbols.

P is (informally) the class of all problems that have polynomial-time algorithms. For simplicity, we focus on decision problems (those having a yes-or-no answer).

Formally: P is the class of all sets L ⊆ {0, 1}n for which there exists a polynomial-time algorithm A such that A(x) = 1 iif x ∈ L.

NP (Nondeterministic Polynomial-Time) is (informally) the class of all problems for which a solution can be verified in polynomial time.

Formally: NP is the class of all sets L ⊆ {0, 1}n for which there exists a polynomial-time Turing machine M, and polynomial p, such that ∀x ∈ {0, 1}n : x ∈ L iff ∃y ∈ {0, 1}p(n) s.t. M(x, y) accepts (here, x is the instance of the problem and y is some solution to the problem).

Why is it called “nondeterministic polynomial-time”? It’s a somewhat archaic name, but we’re stuck with it now. The original idea was that you would have a polynomial-time Turing machine that can make nondeterministic transitions between states, and that accepts if and only if there exists a path in the computation tree that causes it to accept. (Nondeterministic Turing machines
are just like the nondeterministic finite automata we saw before.)

This definition is equivalent to the formal one above. First have the machine guess the solution y, and then check whether y works. Since it is a nondeterministic Turing machine, it can try all of the possible y’s at once and find the answer in polynomial time.

How 30 Lines of Code Blew Up a 27-Ton Generator

Source: Wired, Oct 2020

A secret experiment in 2007 proved that hackers could devastate power grid equipment beyond repair—with a file no bigger than a gif.

… with just a few lines of code, you can create conditions that were physically going to be very damaging to the machines we rely on.

THE TEST DIRECTOR read out the time: 11:33 a.m. He checked with a safety engineer that the area around the lab’s diesel generator was clear of bystanders. Then he sent a go-ahead to one of the cybersecurity researchers at the national lab’s office in Idaho Falls to begin the attack. Like any real digital sabotage, this one would be performed from miles away, over the internet.

The test’s simulated hacker responded by pushing roughly thirty lines of code from his machine to the protective relay connected to the bus-sized diesel generator.

 

Internet Asymmetry

Source: NY Times, Aug 2020

In China, the foreign equivalents of TikTok and WeChat — video and messaging apps such as YouTube and WhatsApp — have been banned for years. The country’s extensive blocking, censorship and surveillance violate just about every principle of internet openness and decency. China keeps a closed and censorial internet economy at home while its products enjoy full access to open markets abroad.

The asymmetry is unfair and ought no longer be tolerated. The privilege of full internet access — the open internet — should be extended only to companies from countries that respect that openness themselves.

Behind the TikTok controversy is an important struggle between two dueling visions of the internet.

The first is an older vision: the idea that the internet should, in a neutral fashion, connect everyone, and that blocking and censorship of sites by nation-states should be rare and justified by more than the will of the ruler.

The second and newer vision, of which China has been the leading exponent, is “net nationalism,” which views the country’s internet primarily as a tool of state power. Economic growth, surveillance and thought control, from this perspective, are the internet’s most important functions.

China, in furtherance of this vision, bans not only most foreign competitors to its tech businesses but also foreign sources of news, religious instruction and other information, while using the internet to promote state propaganda and engage in foreign electoral interference.

Though China is the pioneer of net nationalism, it is on the rise elsewhere, particularly in nations like Saudi Arabia and Iran and, more recently, Turkey and India.

Few foreign companies are allowed to reach Chinese citizens with ideas or services, but the world is fully open to China’s online companies.

From China’s perspective, the asymmetry has been a bonanza that has served economic as well as political goals. While China does have great engineers, European nations overrun by American tech companies must be jealous of the thriving tech industry that China has built in the absence of serious foreign competition (aided by the theft of trade secrets).

We need to wake up to the game we are playing when it comes to the future of the global internet. The idealists of the 1990s and early ’00s believed that building a universal network, a kind of digital cosmopolitanism, would lead to world peace and harmony. No one buys that fantasy any longer. But if we want decency and openness to survive on the internet — surely a more attainable goal — the nations that hold such values need to begin fighting to protect them.

Coders

Source: Marginal Revolution, Mar 2019

The list of small-person or one-person innovators is long…[long list follows]…

The reason so few people can have such an outsize impact, Andreessen argues, is that when you’re creating a weird new prototype of an app, the mental castle building is most efficiently done inside one or two isolated brains. 

The 10X productivity comes from being in the zone and staying there and from having a remarkable ability to visualize a complex architecture. 

“If they’re physical capable of staying awake, they can get really far,” he says.  “The limits are awake time.  It takes you two hours to get the whole thing loaded into your head, and then you get like 10 or 12 or 14 hours where you can function at that level.”  The 10Xers he has known also tend to be “systems thinkers,” insatiably curious about every part of the technology stack, from the way currents flow in computer processors to the latency of touchscreen button presses.  “It’s some combination of curiosity, drive, and the need to understand.  They find it intolerable if they don’t understand some part of how the system works.”